2025-06-18：仅含置位位的最小整数。使用 go 语言编写，给定一个正整数 n，找出一个大于或等于 n 的最小整数 x，且该整数的二进制形式中 1 的数量等于指定的“置位”数目。换句话说，x 的二进制表示中包含固定个数的 1，并且 x ≥ n，目标是找到满足这些条件的最小 x。

示例：

输入：n = 5
输出：7
说明：
7 的二进制为 "111"，恰好有三个 1，且是最小不小于 5 的此类数。

题目来源：力扣第 3370 题。

解题思路（假设本题要求的是最小的全为 1 的数且 ≥ n）

1. 计算 n 的二进制长度：
   • 使用 bits.Len(uint(n)) 获取 n 的二进制位数（即最高有效位的位置）。
   • 举例：当 n = 5（二进制为 101），bits.Len(5) 返回 3。

2. 构造全为 1 的数字：
   • 若二进制中有 k 个连续的 1，则其十进制值为 2^k - 1。
   • 如 k=3 时，2^3 - 1 = 7（即 111）。

3. 判断是否满足条件 x ≥ n：
   • 若 2^k - 1 ≥ n，直接返回该值。
   • 否则需将位数加 1 再构造新的全 1 数。
   • 示例：若 n=8（二进制 1000），其位数为 4，则 (1（1111），15 ≥ 8，返回 15。
• 示例：若 n=5，位数为 3，则 (1，7 ≥ 5，返回 7。

时间复杂度与空间复杂度分析

• 时间复杂度：
• bits.Len(uint(n)) 是常数时间操作（通常由底层硬件指令实现）。
• 构造 (1 同样是 O(1)。
• 整体时间复杂度为 O(1)。

• 空间复杂度：
• 仅使用几个变量存储中间结果。
• 空间复杂度也为 O(1)。

总结

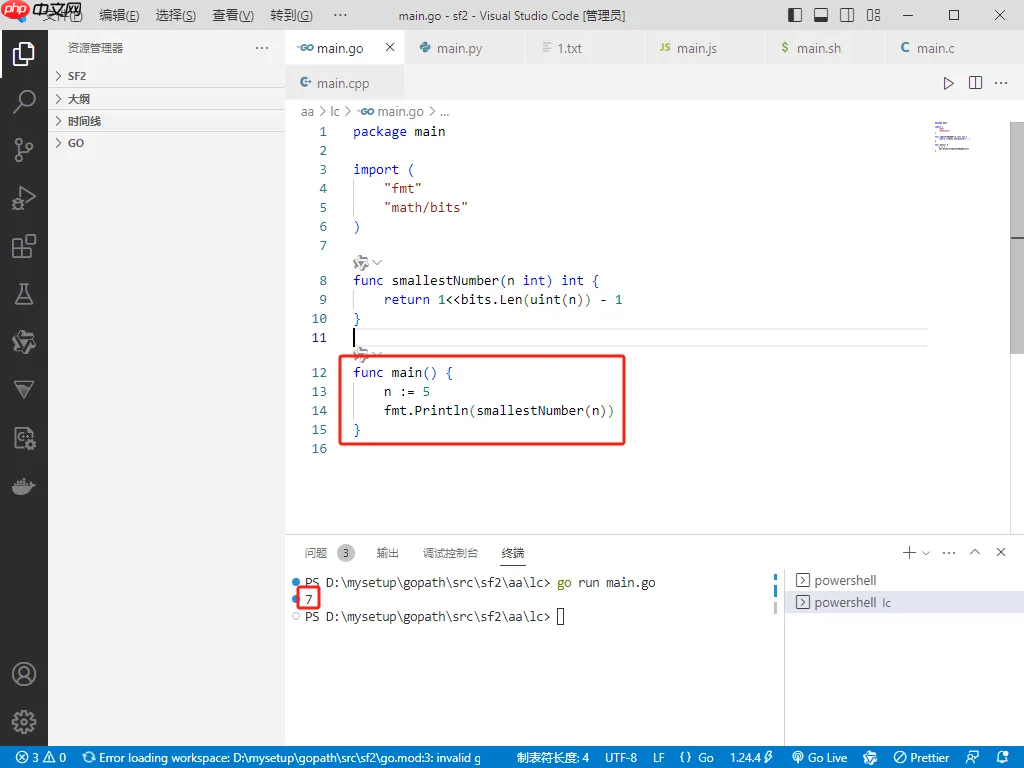
• 此题本质是寻找不小于 `n` 的最小全 1 二进制数。 • 核心方法是通过 `bits.Len` 得到位数 k，然后计算 `(1Go完整代码如下：

package main
import (
"fmt"
"math/bits"
)
func smallestNumber(n int) int {
k := bits.Len(uint(n))
candidate := (1 << k) - 1
if candidate >= n {
return candidate
}
// 如果不够大，则尝试下一位长度
return (1 << (k + 1)) - 1
}
func main() {
fmt.Println(smallestNumber(5)) // 输出: 7
}

Python完整代码如下：

# -*- coding:utf-8 -*-
def smallest_number(n: int) -> int:
						
bits_len 表示 n 的二进制位数
bits_len = n.bit_length()
candidate = (1 << bits_len) - 1
if candidate >= n:
    return candidate
# 如果不够，则尝试更高一位
return (1 << (bits_len + 1)) - 1
测试
print(smallest_number(5))  # 输出: 7
立即学习“go语言免费学习笔记（深入）”；